The Tail Is Wagging The Stock Market Dog
Ignore the daily market narratives.
It’s the options market that drives prices.
The tail is now wagging the stock market dog.
It is not the noise or narratives fed to us by our favourite financial media outlets that drives the daily prices movements in the markets. No. It is the options market, specifically, the actions of market makers and dealers therein who can claim such responsibilities. Fortunately, those of us with an understanding and insight into such matters can put this information to good use within their trading. What follows is an explanation of the dynamic of option dealers hedging activities driving prices, its uses, relevance and consequences for investors. Market making hedging activities has become perhaps the most powerful force in markets today.
So what’s the story?
When investors, institutional or otherwise, buy or sell options they are doing so by purchasing said options from a market maker or dealer. Unlike traditional equity market exchanges whereby investors largely transact directly with one another, the transactions within the options markets is almost exclusively conducted with a dealer taking the opposite side of the trade. Their aim is to make a profit off the bid-ask spread and will attempt to hedge away any direction movement in the underlying.
For example, if a large institutional portfolio manager (let’s call him Ernie) purchases a series of put options as a way of providing downside protection for his assets under management, it is a dealer who is selling these put options to Ernie. Due in part to regulatory changes post-GFC, Ernie has no choice but to have some form of insurance as a way to preserve the capital of his investors. Given insurance is inherently expensive, partly due to said regulatory requirements, Ernie purchases far out of the money (OTM) put options on the S&P 500 as a way to reduce the premiums he will pay to buy these options.
Conversely, in the low-yielding landscape encompassing todays financial markets, Ernie will jump at any chance he can to reach for a little extra yield to boost his P&L. Given the impressive returns generated by call-overwriting strategies over the past decade, Ernie is happy-as-Larry to deploy such a strategy. He does this by selling out of the money calls on the S&P 500, collecting a nice premium for his troubles. Call-overwriting has become one of the most popular strategies of asset managers over recent years; and is the premise of the ever so popular short-volatility trade.
By buying and selling options to investors, the dealers expose themselves to movements in the price of these options on their books, and will thus look to delta-hedge their exposure by buying or selling the underlying in order to remain delta-neutral, removing any directional exposure to the movements in the assets underlying their options book. The delta of an option is a measure of how much the option price will change per unit of change in the underlying asset. The dealers goal is to buy or sell this underlying asset (i.e. the S&P 500) in such a way that they are able to replicate the payoff of the options on their books. The higher the dealers delta exposure, the greater amount of hedging via the underlying is required.
Returning to the above example, if the call option sold by Ernie is a 50 delta call (i.e. has a delta of 0.50), then the market maker is long the call (thus long the index) and will hedge this position by shorting the S&P 500 to such a degree that their delta exposure is reduced to nil. Likewise, when Ernie purchases a -20 delta put from the market maker, this leaves the dealer with a short put position (again equivalent to being long the market), requiring them to short the underlying, however to a lesser extent in this case as the delta for a far OTM put is lower (i.e. less negative for put options) compared to a put or call option that is closer to its strike.
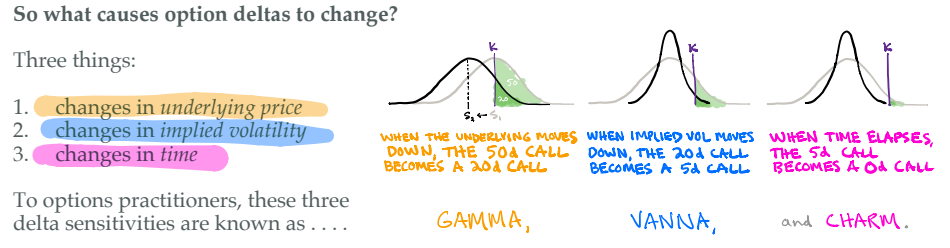
When the delta of an option changes, the dealers will be forced to either buy or sell the underlying asset in order to retain their delta neutral position. There are three factors responsible for movements in delta: a movement in its underlying price (“Gamma”), a change in the implied volatility of the asset or index (“Vanna”), or a change in the time to expiration of the option (“Charm”).
For all those visual people out there, this colorful chart below is a nice illustration of our three amigos:
This is where the fun begins.
…and Gamma is?
Gamma is delta’s sensitivity to a change in price of the underlying asset. As delta is a measure of the sensitivity in the price of the option itself relative to a change in price of the underlying; gamma measures delta’s sensitivity to changes in the underlying (making gamma a derivative of delta). Delta is not a constant. When the price of a stock moves up or down, the delta also changes relative to the moneyness of the option. Gamma measures the rate of change of delta. From the perspective of an options dealer, gamma exposure determines their hedging and re-hedging requirements to remain delta neutral. Gamma matters for dealers (a lot!).
This process of dealers re-hedging their books can be tricky. It is particularly dependent on how far out of the money the options on their books are at any point in time. When the majority of options on their books are only slightly OTM (i.e. when the dealers are predominately long slightly OTM calls due to the yield enhancing strategies deployed by Ernie and his fellow fund managers), and as a result these deltas are more sensitive to changes in the underlying as they are closer to their strikes compared to their short put positions. It is in such situations that dealers are long gamma (being highly exposed to movements in the underlying), and in order to hedge their books they need to buy the underlying as the index falls and sell the underlying as the market rises.
Dealers being long gamma has the effect of stifling price movements and thus dampening volatility. When dealers are short gamma, this has the effect of amplifying market volatility. We can see below how when gamma exposure is positive, immediate market moves are highly constrained, whilst when gamma exposure is negative, prices can move quickly to the upside or downside.
Having an understanding of whether dealers are long or short gamma gives investors a powerful tool to predict short-term volatility and upside or downside potential in prices.
An example!
Let us once again return to our trusted portfolio manager, Ernie. He has just sold a bunch of slightly OTM call options to harvest some additional yield, and purchased some significantly OTM put options to protect his downside risk. Let’s pretend these calls have strike of $105, the puts a strike of $90 and the index is currently trading at $100. Given the dealer is now long call options and short put options, and we now know their job is remain market neutral; they will buy and sell an appropriate amount of the underlying index so an increase or decrease in the value of their short puts and long calls does not result in any significant loss of their own capital. The dealer will hedge their long call exposure by selling the underlying index, and will hedge their short put exposure by also selling the underlying.
However, as the puts are currently far out of the money, the delta of these options is low and thus does not require significant hedging by the dealer. However, as the call options are much closer to their strike price, their delta’s will be higher and also more sensitive to the underlying index’s change in price (long gamma!). With the index trading at $100, the dealer will need to short a fair amount of the underlying index to remain delta neutral. When the dealers long call options are dominating their hedging requirements, they will be buyers of the underlying as prices fall (i.e. reducing their short positions) as their long calls lose value and deltas fall. Conversely, when prices rise and the spot reaches or exceeds the $105 strike, they will be sellers of the underlying (i.e. increasing their short positions) as the call options increase in value and deltas increase.
So, let’s say Ernie sold 1000 contracts of the $105 strike calls, and purchased 1000 of the $90 strike puts. Utilising the classic Black-Scholes formula, and assuming the options are pricing implied volatility at 20% with one month to expiration and the risk free rate is nil, we are able to roughly estimate the actual dollar hedging obligations by the dealers as a result of Ernie’s activities. By putting this information into the formula and adjusting for changes in the spot price, we can visually see how their hedging requirements change:
Whilst the above table may appear intimidating, what matters is how the total short underlying position of the dealers changes as the spot price changes. As the spot rises from $100 to $105, the dealers must increase their short positions by roughly $3m (i.e. $2.3m increases to $5.4m), and when the spot rises to $110, they must again increase their short positions by an additional $3.3m. Conversely, when the spot falls back from $110 to $105, they are able to reduce their short positions by this $3.3m. This is what happens when dealers are long gamma and the deltas are highly sensitive to changes in the underlying; they increase their shorts as prices rise and reduce their shorts as prices fall.
Gamma exposure is highest when their long call options dominate their books and the spot price is closest to the strike price, resulting in dealers constantly trading against the market, and thus providing liquidity. This process of buying dips and selling rallies works to stifle volatility.
On the other hand, when the spot falls from $100 to $95 and then to $90, the hedging requirements for the dealers long call options is greatly reduced, as it is the deltas of their short put options (thanks to Ernie’s buying of insurance) that begin to dominate their books. As the spot moves from $95 to $90, the dealer is required to increase their short position by $2.4m. Indeed, as the spot continues to fall to $85, a further $2.6m is required to be shorted by the dealer. This is when dealers are short gamma and they are trading with the market. Falling prices begets further shorting which further pushes prices down. The simple act of buying insurance as prices fall only acts to accelerate further selling (gamma squeeze!). This constant re-hedging by dealers is the predictive power of gamma.
The values used in this example are merely for illustrative purposes only. In truth, the buying and selling pressure of dealers in dollar terms for the S&P 500 can be upwards of $10-$15 trillion when gamma exposure is high. This is a market phenomenon whose impact continues to grow.
Gamma and OPEX
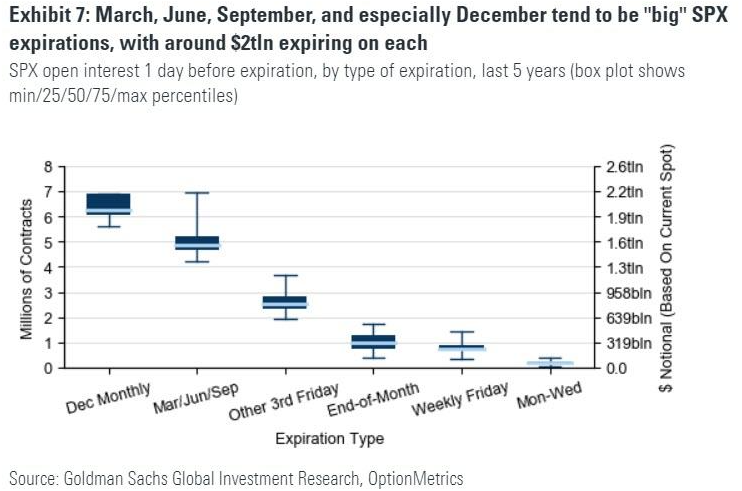
When it comes to gamma exposure, options expiration (OPEX) dates matter. OPEX often marks decisive turning points in the markets. When gamma exposure is high and the S&P 500 is slowly creeping up in price, such a move will generally end when gamma exposure falls off dramatically around OPEX. Likewise, when gamma exposure is low and markets are falling or volatile, such a regime we seemingly end come OPEX. On days of options expiration, the dealers delta and gamma exposure will often change significantly, which can cause quick upside or downside moves in the market as the dealers rapidly increase or decrease their hedges. This is particularly prominent on the larger monthly and quarterly OPEX dates, where open interest and option activity is at its highest.
This makes sense. Given how the most open interest in options are for those with the nearest monthly expiration, the majority of the dealers hedging activities would be incumbent on their delta exposure to the nearest expiration. Let’s use the February/March COVID induced market rout as an illustration. The January 2020 options expiration on the 17th was met with a fairly significant fall in dealers gamma exposure, preceding what was a fairly bumpy week or two in prices. Fortunately, this dip was bought quickly by investors (we can see this by looking at the high level of dark pool buying at the time), and an unwillingness for investors to hedge their downside risk by buying put options for protection. Such a combination saw gamma exposure soar back up once again, allowing the index to resume its steady march upwards.
The index would enjoy a fairly stable period seeing out the final weeks until the February OPEX would come around on the 21st. So what happened this time? Remember, when dealers gamma exposure is low or near zero, their hedging requirements do not have much directional impact on market prices. It is during these periods that traditional market forces are able to more easily assert themselves. Unlike during January’s dip, we did not see any real buying pressure from discretionary investors. Portfolio managers like Ernie seemingly had finally caught up with the idea that this COVID thing might actually matter. Not only did this bearish sentiment consuming Wall Street lead to investor selling, but it was the increases in their downside protection buying of put options during this time that saw dealers gamma exposure turn negative. This is when things got real ugly real fast, and we all know what happened next.
When gamma exposure is negative and dealers books are predominately being dictated by their short put positions, they are required to short the underlying (but you knew this already by now!). As prices continued to fall post February OPEX and their short put positions were increasingly in the money, they were required to sell more and more of the underlying.
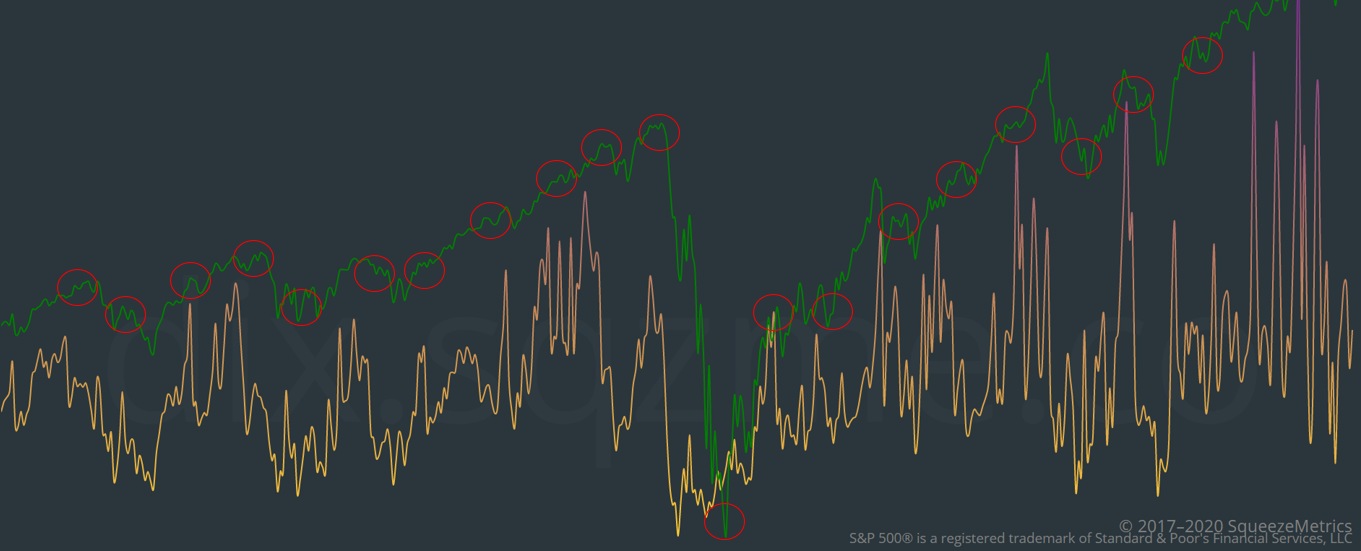
The below chart illustrates this visually. The circled points represent the monthly OPEX dates. Note how these points in time generally coincide with turning points in the market.
We can see above how the February 2020 OPEX coincided with a fall in gamma exposure (gold line), allowing the market to correct and then acting to reinforce the sell-off. You will also note the market bottom in March also coincided with the March OPEX. Coincidence? I think not. When March OPEX finally rolled around and the dealers short put positions were finally off their books, they were able to buy back their shorts, thus kicking off the rally that ensued.
Gamma squeeze!
The dynamic of negative gamma exposure causing volatile swings in prices not just on the downside but the upside too is what has become known as a “gamma squeeze”. Remember, when dealers delta hedging obligations are primarily being determined by their short puts that are in the money or at the money, dealers are short gamma. However, dealers can also be short gamma when another situation rises. Whilst not common on general indices such as the S&P 500, when speculation is rampant on certain individual stocks and investors are buying call options at record levels, such a scenario may cause a gamma squeeze to the upside. Suppose a group of disgruntled millennials identify an opportunity to take advantage of such predictive buying obligations of dealers. This dynamic could be particularly powerful when a targeted company is fairly illiquid, and whose float has a large percentage of short-interest (…yes I’m taking about you Gamestop).
If the dealers are primarily short OTM calls, then they are short the stock and will hedge by buying the underlying. Then if the price of the stock rises and the delta of their short calls increases, you guessed it - they will be required to increase their hedges by buying more of the underlying, pushing prices up in a self-reflexive spiral. A gamma squeeze combined with a short squeeze is an especially powerful combination. Weaponized gamma is a thing!
Gamma exposure… one more time.
In its simplest form gamma exposure can be interpreted as this; when gamma exposure is high (dealers are long gamma), their hedging requirements result in low volatile moves in prices as dealers trade against the market, providing liquidity. When gamma exposure is negative (dealers are short gamma), they will trade with the market, amplifying volatility and directional moves.
The relationship between gamma exposure and subsequent returns is clear and powerful.
Vanna and Charm
Let’s turn our attention to gamma’s lesser known accomplices, vanna and charm. To refresh, the delta of an option is not only impacted by movements in the underlying (gamma), but also by changes in implied volatility (vanna) and changes in the time to expiration (charm). The effects of vanna and charm generally work in tandem with one another.
Vanna describes how a change in an options implied volatility influences its delta. As we have discussed, dealers are predominately short calls and long puts, this leads to them being long vanna.
Implied volatility’s role in dealer hedging activities is important, and perhaps just as impactful as gamma. When implied volatility increases, the delta of an option also increases. Conversely, when implied volatility falls. the delta of an option also falls. Given that the VIX term structure is in contango roughly 75% of the time, in most market conditions vanna provides a consistent bid that supports prices.
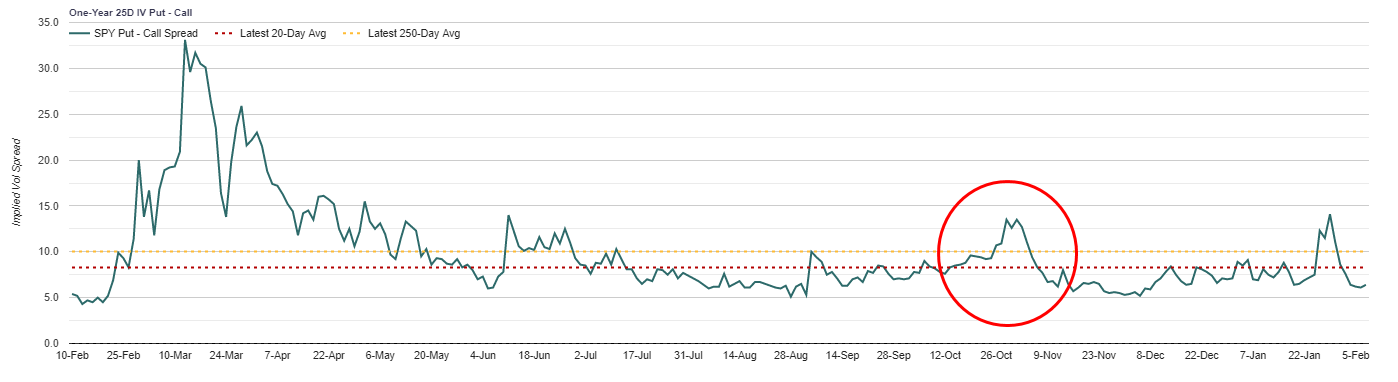
Let’s illustrate vanna’s impact with our trusty portfolio manager, Ernie. Suppose Ernie saw the November 2020 US election as a potential catalyst for markets. With civil unrest abundant and the likelihood of a contested election high, Ernie deemed it wise to load up on downside protection, just in case. This increased buying pressure of put options resulted in the implied volatilities of said options rising, pushing up their deltas.
We can see this visually below, as the put-call implied volatility spread rose just prior to the election.
The dealers, being short these options, are required to undertake their predictive hedging activities by shorting the underlying. The more implied volatilities rise, the more they are required to short. So, when implied volatility peaked days before the election and the VIX started to fall, dealers were able to reduce their short hedges by buying back the underlying. This buying of the underlying puts downward pressure on implied volatility, causing vanna flows into the market as the buying back of dealer shorts continued. Such binary, known events which are deemed as “risky” by investors illustrate the power of vanna. Likewise, this also helps explain why whenever we see sharp rises in volatility, they are generally quick to mean revert.
Again returning to the Black-Scholes formula to illustrate how changes in implied volatility impact dealers delta hedging obligations, we can see this dynamic in play. Once again assuming dealers are long 1000 $105 strike calls, short 1000 $90 strike puts and the spot price is $100, a fall in implied volatility from 50% down to 5% has a significant influence on how much of the underlying dealers are required to short:
It should be noted the above example is largely a simplification to help illustrate how implied volatility impacts delta, in truth vanna is far more dynamic. Moneyness matters with vanna. If the dealers short call positions were in the money (i.e. the spot price was above the $105 strike), then the impact of vanna works in reverse; as implied volatility falls, the delta of these ITM calls actually increases, resulting in dealers increasing their short hedges. The opposite effect is true for when dealers are short ITM put options. She is a fickle beast vanna.
Charming!
As I mentioned above, vanna and charm have similar effects on delta; generally providing a consistent bid during “normal” market conditions as implied volatility falls and time passes. Charm (sometimes referred to as delta-bleed), is a measure of how the time to expiration of options influences the sensitivity of options to changes in the underlying (delta). The general effect of charm is this; as OPEX approaches, dealers need to hedge a little less every day. You know the saying; “never short the market heading into OPEX”.
For all those OTM puts and calls bought and sold by investors respectively, so long as they remain out of the money, their deltas will decline each and every day simply as a function of time. Let me illustrate this below, returning to the same Black-Scholes example we used for gamma and vanna:
As is evident, a dealer who is short OTM puts and long OTM calls will reduce their short hedges by buying back the underlying simply as a function of time, all else equal. This buying pressure of charm is particularly powerful as the options are closest to expiration, whilst also have a profound effect on quarterly OPEX dates which generally tend to have a greater level of open interest.
When markets are calm and there are no significant price movements in the underlying, it is vanna and charm who are largely responsible for the slow grind upwards we see so often during periods of high gamma.
A market force only getting stronger
The delta-hedging activities of dealers represent an ever increasing part of underlying flows into and out of securities. Due to the increasing level of options strategies deployed by institutions, along with the growing popularity of options among retail investors, the supply and demand forces that drive markets are becoming increasingly controlled by these non-discretionary flows. This is not to say traditional fundamental flows cannot direct markets, but it means their ability to drive prices can be restricted or enhanced, depending on what the options market allows.
The year that was 2020 will perhaps be remembered best for the extreme rise in retail investors use of options as a means to speculate, and is a prime example of how the mechanics of gamma, vanna and charm can drive markets.
Furthermore, as I have written about previously, the reduced liquidity of markets over recent decades and increasing volatility due to the rise of passive investing, will only work to amplify the effects of dealer hedging. We truly live in a world where the stock market tail is wagging the dog.
If liquidity continues to fall and the use of options continues to rise, then so long as dealers continue to delta hedge their positions to remain market neutral, their flows into and out of assets will become and increasing part of overall transactional volume and will continue to impact prices. The effects of gamma, vanna and charm are not going anywhere any time soon. It is important to understand that markets no longer move in ways that we have seen historically.
Putting it all together
In closing, here are some important points investors and traders should keep in mind:
Due to their delta hedging obligations, dealers are in effect committed to a predictable regime of buying and selling.
When dealers are long gamma; they will provide liquidity and stifle volatility. This occurs when dealers are predominately long options. When they are short gamma, dealers are taking liquidity and exacerbating price movements. This occurs when dealers are predominately short options.
The vast majority of the time, dealers are short puts and long calls. The significance of these positions varies depending on the open interest and whether their delta hedging activities are being driven by the deltas of their short puts or long calls.
A common effect of high gamma exposure in a bullish market is to maintain a slow crawl upward in prices. As implied volatility falls and options expiration approaches, dealers will have to short less and less each day, providing vanna and charm flows to support prices.
The best risk/reward opportunities come when gamma exposure is low or negative, as the options market is able to squeeze prices higher in a volatile manner.
The effects of gamma, vanna and charm tend to change significantly once OPEX has come and gone, and generally marks turning points in the markets.
As I have discussed, these market forces are only being enhanced by the increasingly fragile nature of markets. Fortunately, adept traders can use this valuable information to their advantage. Some of the best strategies come as a result of market participants being forced to act in certain ways. An awareness of gamma exposure, options expiration dates and the like are highly advantageous for traders and investors. Such services and platforms like SqueezeMetrics provide such information for retail investors to put to use. Best to take advantage.
If you enjoyed what you are reading, I encourage you to subscribe to my blog, Acheron Insights. Your support is greatly appreciated.